Modelling Groundwater Arsenic Contamination in China with the Groundwater Assessment Platform (GAP)
Background
This is the summary of the bachelor thesis of Ruth Arnheiter, student of Natural Resource Sciences at the Zurich University of Applied Sciences, ZHAW, Switzerland. Arsenic (As), occurring as a natural contaminant in groundwater, threatens the health of over 100 million people worldwide (Smedley & Kinniburgh, 2002). Prediction maps can help policymakers better identify areas at risk. In 2013, Lado et al. used logistic regression to create a prediction map of arsenic pollutants in China, basing their model on environmental variables according to the following five categories: geology, surface soil, topography, hydrology and gravity. They defined areas at high and low risk with respect to arsenic pollution by running 100 stepwise logistic regressions. Hence, the technique was not easily reproducible, especially for non-professionals. With GAP, prediction maps can be produced significantly faster and easier. But few modelling examples were available and so its sensitivity had not been determined. This bachelor thesis was focused on the demonstration and explanation of the capabilities of the platform, by (i) using GAP to produce an arsenic hazard map of China, comparable to that provided by Lado et al., (ii) analysing the differences between the two maps, and (iii) analysing the sensitivity of GAP by determining the number and kind of independent data needed to produce an effective prediction map.
Methods
Modelling process in GAP
Data. For their survey Lado et al.’s used 2668 arsenic measurements and eight environmental variables (Holocene sediments, saline soils, subsoil texture, topographic wetness index (TWI), slope, density of rivers, distance to rivers and gravity). For modelling in GAP, Lado et al.’s 2668 arsenic measurements were used as well but the latter four variables were excluded because of technical requirements of the platform, high correlations between slope and TWI, and the results of stepwise logistic regression. In addition, Lado et al. validated their model with a separate data set of 625 measurement data. “Modelling.” Logistic regression was calculated with the WHO safety guideline for arsenic in drinking water of 10 µg/L and run once. The generated prediction model (modelGAP) was transferred to ArcGIS.
Table 1: Summary of measurement data, validation data, number and kind of variables and modelling approach in GAP and in Lado et al.’s study.
| GAP | Lado et al. | |
|---|---|---|
| Measurement data | 2688 | 2688 |
| Validation data | - | 625 |
| Number of variables | 4 | 8 |
| Variables | Holocene sediments
Saline soils Subsoil texture TWI |
Holocene sediments
Saline soils Subsoil texture TWI Slope Density of rivers Distance to rivers Gravity |
| Modelling | 1 Stepwise log. regression
1 logistic regression |
100 Stepwise log. regressions |
Difference analysis between the models created in GAP and in Lado et al.'s study
Probability maps. In ArcGIS (version 10.4), modelGAP was aligned to the same grid with Lado et al.’s prediction map (modelLado) for accurate comparison. The correlation of the probabilities of modelGAP and modelLado were calculated with the band collection statistic tool in ArcGIS. Binary maps. The models were binary coded using the cut-off values of 0.41 for modelGAP and 0.46 for modelLado. The cut-off for modelGAP was compiled in GAP by evaluating the trade-off of sensitivity (ability to correctly classify predictions above chosen threshold) and specificity (ability to correctly classify predictions below chosen threshold). The cut-off of 0.46 was determined by Lado et al. using the ROC curve (Rodríguez-Lado et al., 2013). The differences of the two binary models were located by subtracting one model from the other and the differences in percentages were calculated and compared to the prediction map. In addition, the localised differences were compared with the probability map to better understand the relation between the differences and the predicted probabilities. To estimate the influence of the cut-off modelGAP was again binary coded with the cut-off of 0.46 and processed as previously.
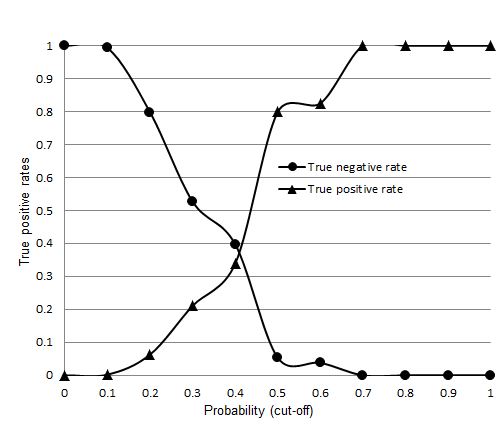
Figure 1: Trade-off of true negative and true positive rates of the logistic regression for modelGAP revealed in GAP.
Sensitivity analysis of GAP
Number of measurement data. Once a suitable model using all 2668 measurement data was created, the effect of using fewer measurement data was tested. Randomly selected subsets of the 2668 measurement data were retrieved (250, 500, 750, 1000, 1250, 1500 and 2000 data) in threefold repetition. In addition, a data set of 3318 measurement data was aggregated from 2668 measurement data and 625 validation data used in Lado et al.’s study. There was an addition of 25 measurement data which might have been generated by the previous aggregation of the measurement points to 1 km2 resolution. Each data set was processed according to the previous calculations with stepwise logistic regression to calculate the relative and binary correlations using the corresponding cut-offs compiled in GAP. In addition, for a better understanding of the vulnerability of the correlations, the model with 1250 measurement data was recalculated in tenfold repetition.
Number and kind of variable. To examine the effect of using fewer variables on the modelling, the validity of all combinations of the four variables used in ModelGAP (Holocene sediments, saline soils, subsoil texture, TWI) were analysed by comparing the corresponding AUC. Every combination of variables was joined with the 2668 measurement data to run a logistic regression. To prove that non-related variables produce an AUC around 0.5, the 2668 measurement data was joined with a random variable temperature to calculate the corresponding AUC.
Results
Probability model created in GAP
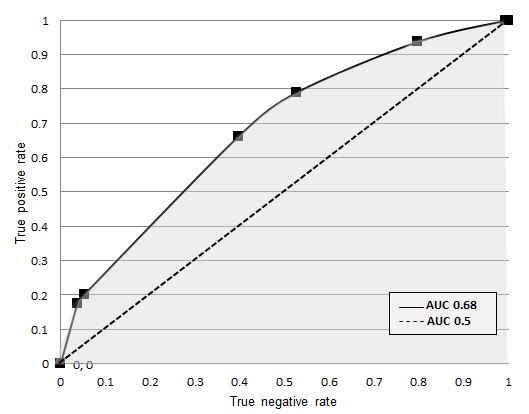
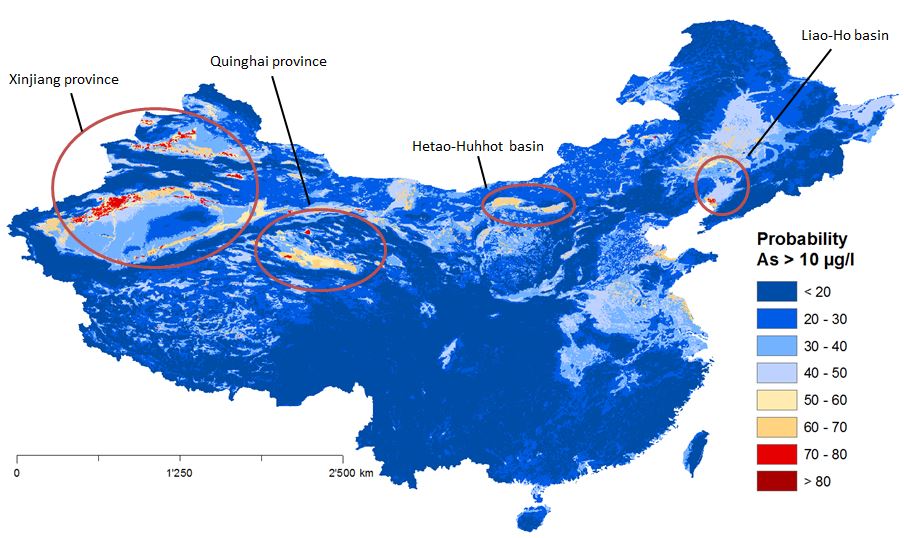
In modelGAP, all variables showed p-values < 0.01, except for soil texture which presented a p-value of 0.03 (Table 2). Highest coefficient showed saline soils (0.88), followed by Holocene sediments (0.73), soil texture (-0.25) and TWI (0.18) (Table 2). Besides, soil texture showed a negative coefficient. The AUC of the model was 0.68. ModelGAP showed probabilities between 20 - 80% (Figure 3). High risk areas were determined in the Xinjiang and Quinghai province, Hetao-Huhhot and Liao-Ho basin.
Table 2: P-values of all variables used calculated by GAP. P-values of 0 are most probably due to rounding errors in GAP.
| Variable | p-value | coefficients |
|---|---|---|
| Holocene sediments | 0 | 0.73 |
| Saline soils | 0 | 0.88 |
| Soil texture (clayey soils) | 0.031 | -0.25 |
| TWI | 0 | 0.18 |
Figure 2: Receiver Operating Characteristic Curve (ROC) of modelGAP and the corresponding area under the curve (AUC) retrieved in GAP.
Figure 3: Prediction map of arsenic probability greater than 10 µg/l in China produce with GAP. Circles indicate areas with high risk probabilities.
Analysed differences between modelGAP and modelLado
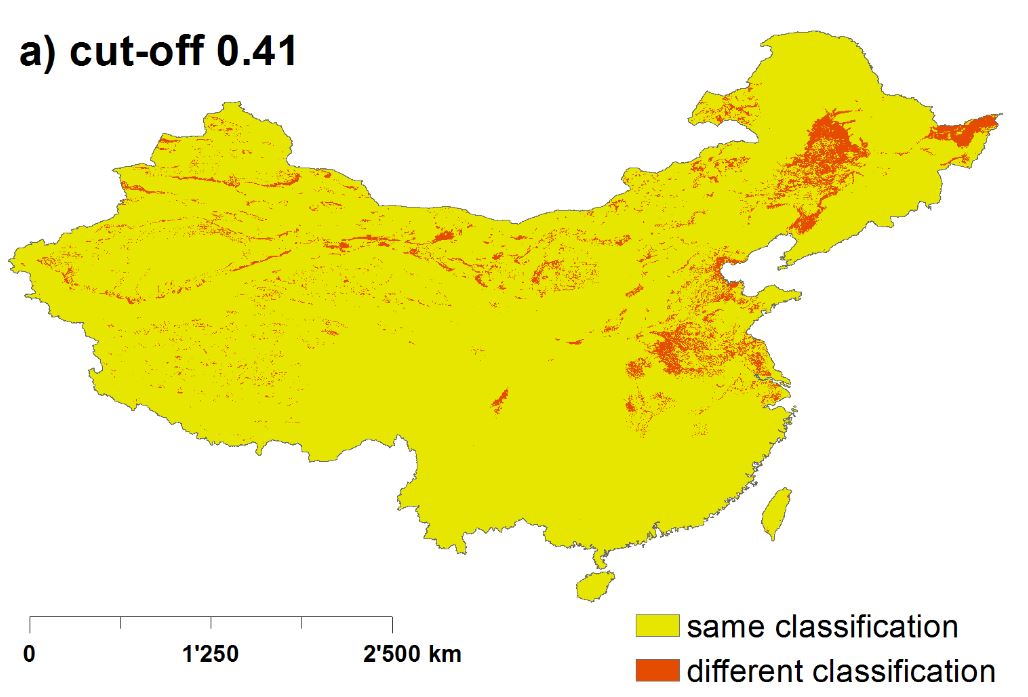
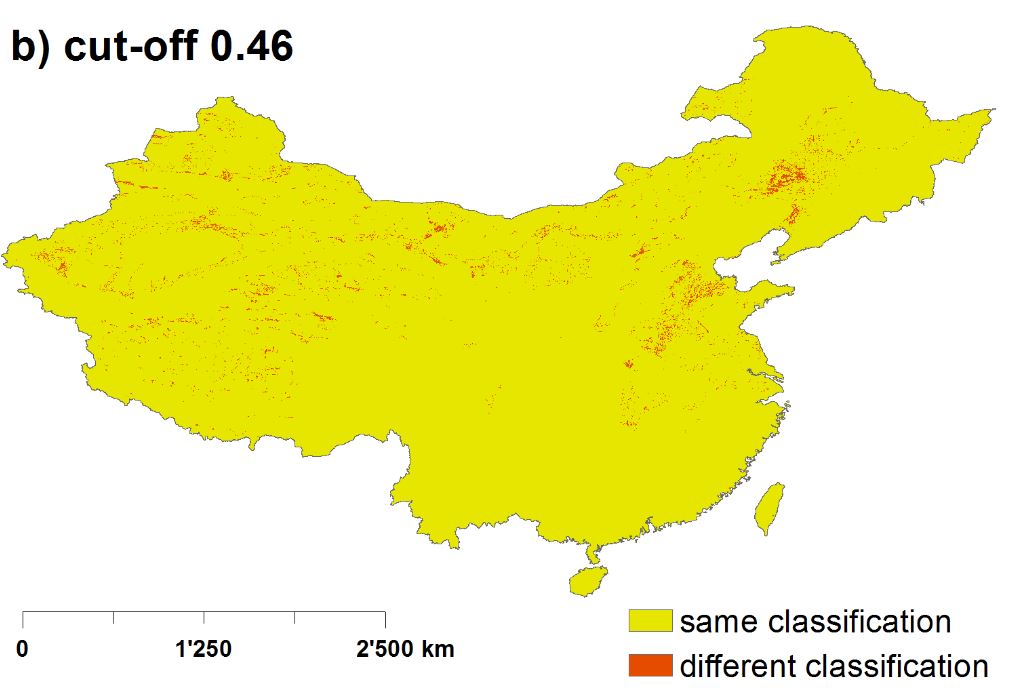
The probabilities of modelGAP and modelLado were highly correlated (0.97) (Table 3). The binary model using the cut-off of 0.41 for modelGAP differed in 6% of the areas (Figure 4). 95% of these differences lied in areas with predicted probabilities of high arsenic contamination in groundwater between 40 – 50%. Using the cut-off of 0.46 for modelGAP, the two binary modelGAP and modelLado were brought more in line. The differences became smaller; in fact, as low as 1.5%.
Table 3: Correlation between the probability modelGAP and modelLado and congruence (%) between the binary models with the cut-off 0.41 and 0.46 for modelGAP.
| Correlation
ModelGAP (probability) |
Congruence (%)
“ModelGAP” “(binary; cut-off 0.41” |
Congruence (%)
“ModelGAP” “(binary; cut-off0.46)” | |
|---|---|---|---|
| ModelLado>
(probability) |
0.97 | - | - |
| ModelLado
(binary; cut-off 0.46) |
- | 6 | 1.5 |
Figure 4: Localised differences between the binary modelGAP and modelLado (a) with the cut-off 0.41, and b) with the cut-off 0.46.
Analysed sensitivity of GAP
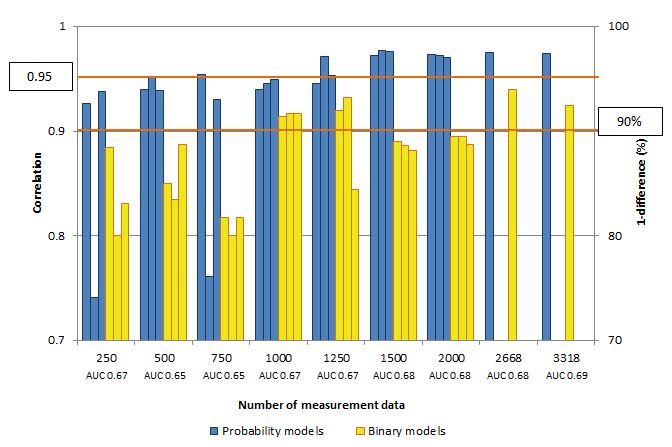
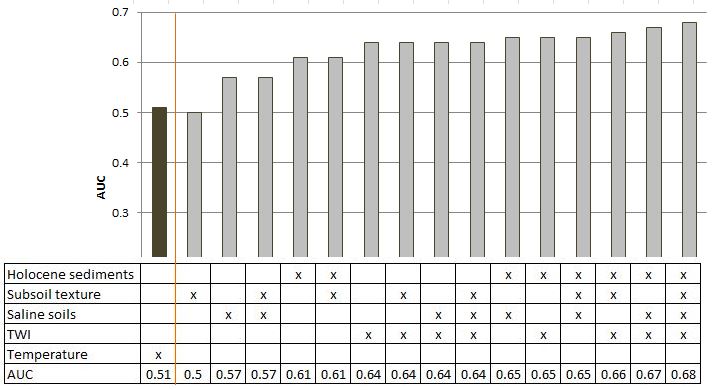
As expected, the best result was achieved with 2668 measurement data. Most of the randomly selected subsets above the number of 1000 measurement data showed similar results compared to the initial 2668 measurement data. The probability models were well correlated (0.95), the binary models were congruent at 90% and the AUC was not smaller than 0.67 for any data set (Figure 5). Data sets lower than 1000 measurement data achieved less reliable results, considering means, variations and AUCs. In addition, the data set of 1250 measurement data showed great variations, especially with the binary models. This variation, however, decreased if the calculations were repeated multiple times. Testing the number of required variables showed that the best result was achieved with the initial four variables, namely Holocene sediments, saline soils, subsoil texture, and TWI (0.68) (Figure 6). The smallest AUC was shown with the variable subsoil texture (0.5). An AUC of 0.65 was achieved by using either three variables (Holocene sediments, subsoil texture and saline soils) or two variables (Holocene sediments and TWI or Holocene sediments and saline soils), while temperature showed an AUC of 0.51, indicating that temperature does not contribute to arsenic contamination in groundwater.
Figure 5: Correlations of probability modelGAP and modelLado (blue) and 1-difference (%) of the binary models (yellow) as well as the corresponding AUC of different data sets of 250, 500, 750, 1000, 1250, 1500 and 2000 data in threefold repetition and of the original data set of 2668 data as well as the data set of 3318 data with one repetition.
Figure 6: Summary of AUCs of all combinations of the four variables Holocene sediments, saline soils, subsoil texture, TWI used for modelGAP.
Discussion
GAP predicted the same areas to be high risk areas as Lado et al. Holocene sediments, saline soils, subsoil texture and TWI are indeed the more important variables, compared to slope, density of rivers, distance to rivers and gravity, as used in Lado et al.’s survey (Rodríguez-Lado et al., 2013). The inverse relation of subsoil texture showed that the presence of clayey soils decreases the probability of arsenic in groundwater. The best achieved AUC in GAP was 0.68, which is considered to be too low for a good prediction model (Hosmer, Lemeshow, & Sturdivant, 2013). Nevertheless, GAP produces results as accurate as those of Lado et al. by running only one logistic regression, compared to the 100 stepwise logistic regressions that Lado et al.’s used. Despite the different number of variables (four variables for modelGAP, eight variables for modelLado), the two models’ probabilities were highly correlated (0.97). The binary model with the cut-off of 0.41 slightly differed from the binary model of Lado et al. (6%). Interestingly, almost all localised differences were in areas with risk probabilities between 40 - 50% (95%). Approximating the cut-off for modelGAP to that of modelLado the area of differences decreased to one fourth of the differences revealed with the smaller cut-off (1.5%). Hence, the threshold used for the binary coding is decisive about the correlation of two binary models. Nevertheless, whatever technique was used for the analysis of differences, the two models showed a congruency of 94%, which is high. Most of the randomly selected subsets of the 2668 measurement data showed a similar behaviour compared to the initial data set. As expected, the bigger the data set was, the better the models were correlated. Interestingly, similar results (compared to the 2668 measurement data) were achieved with as little as 1000 measurement data, which is less than 40% of the initial data set. However, these investigations were based on only three repetitions which may not be enough to be conclusive, especial when standard deviations vary, such as for 1250 measurement data. But the investigations with ten repetitions proved that the higher the number of repetitions, the smaller was the variation. The investigation of the variables showed the best results with four variables. Interestingly, in some cases the number of variables did not determine the AUC but rather the composition of the variables. However, all of the combinations out of the four variables produced a smaller AUC than the four variables themselves. Temperature as a variable showed that an AUC of 0.51 indicates non-correlation. Nevertheless, this study does not give final recommendations regarding the number of required measurement data in relation to the area of investigation. For example, downscaling these results to Switzerland, which has a surface area of 41,285 km2 (which is less than 0.5 % of China’s 9,297,000 km2), would mean that less than 0.5% of 1000 measurement data should be sufficient to predict arsenic pollution in Switzerland, which intuitively is insufficient. In the future, investigation on the smallest measurement data set related to the area but still produces reliable results will help policymakers better determine how many measurement points are required. In addition, this survey did not analyse the potential influence of the local distribution of measurement data. Investigating whether such distribution is indeed of importance for the generation of prediction maps should be of considerable interest for further studies.
Conclusion and Outlook
By running only one logistic regression, GAP produces results as accurate as those of Lado et al. who run 100 logistic regressions. The data could even be limited to a certain number of measurement data (1000 measurement data in this survey) as well as to a certain selection of variables (four variables in this survey). The selection of the most important variables was essential though. Therefore, GAP should (i) allow users to add any number of variables and (ii) give information on how GAP defines a variable to fit or not to fit. These improvements of GAP will help users to make the right selection of variables and to better understand the techniques behind the platform, which will enhance GAP’s promotion and dissemination. The following further investigation could be of interest:
- Which is the smallest measurement data set related to the area of interest but still produces reliable results?
- This will help policymakers to determine the number of measurements points required.
- How does the distribution of measurement data affect the probability model?
- This will help policymakers to determine the distribution of measurements points required.
References
Hosmer, D. W., Lemeshow, S., & Sturdivant, R. (2013). Applied Logistic Regression, Third Edition: Willey, New Jersey.
Rodríguez-Lado, L., Sun, G., Berg, M., Zhang, Q., Xue, H., Zheng, Q., & Johnson, C. A. (2013). Groundwater arsenic contamination throughout China. Science, 341(6148), 866-868.
Smedley, P. L., & Kinniburgh, D. G. (2002). A review of the source, behaviour and distribution of arsenic in natural waters. Applied Geochemistry, 17(5), 517-568. doi:Pii S0883-2927(02)00018-5 Doi 10.1016/S0883-2927(02)00018-5